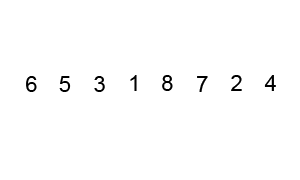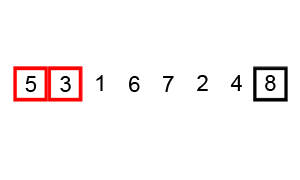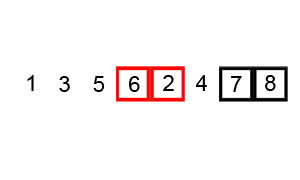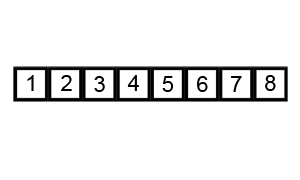Sıralama Algoritmaları
Sıralama algoritması, bilgisayar bilimlerinde ya da matematikte kullanılan, verilen bir listenin elemanlarını belirli bir sıraya sokan algoritmadır. En çok kullanılan sıralama türleri, sayı büyüklüğüne göre sıralama ve alfabetik sıralamadır. C# programlama dilinde sıklıkla kullanılan bazı sıralama algoritmalarının örnekleriyle birlikte detayları:
- Selection sort (seçmeli sırlama)
- Bubble sort (balon sıralaması)
- Insertion sort (eklemeli sıralama)
- Merge sort (birleştirmeli sıralama)
- Quick sort (hızlı sıralama)
– Seçmeli Sıralama (Selection sort) Algoritması
Seçmeli sıralama algoritması, bir diziyi, sıralanmayan kısımdan en düşük elemanı tekrar tekrar bularak ve başa koyarak sıralar.

public void SelectionSort(int[] array)
{
int n = array.Length;
for (int i = 0; i < n - 1; i++)
{
int minIndex = i;
for (int j = i + 1; j < n; j++)
{
if (array[j] < array[minIndex])
{
minIndex = j;
}
}
int temp = array[minIndex];
array[minIndex] = array[i];
array[i] = temp;
}
}
– Kabarcık/Baloncuk Sıralaması (Bubble sort)
Kabarcık Sıralaması, bilgisayar bilimlerinde kullanılan yalın bir sıralama algoritmasıdır. Sıralanacak dizinin üzerinde sürekli ilerlerken her defasında iki öğenin birbiriyle karşılaştırılıp, karşılaştırılan öğelerin yanlış sırada olmaları durumunda yerlerinin değiştirilmesi mantığına dayanır. Algoritma, herhangi bir değişiklik yapılmayıncaya kadar dizinin başına dönerek kendisini yineler. Adına “Kabarcık” sıralaması denmesinin nedeni büyük olan sayıların aynı suyun altındaki bir kabarcık gibi dizinin üstüne doğru ilerlemesidir.
Başlangıçta yer yer değiştirme sıralaması olarak adlandırılan kabarcık sıralaması, dizi içindeki büyük elemanların algoritmanın her adımında dizinin sonuna doğru doğrusal olarak ilerlemesini sağlar. Bu ilerleme, seçmeli sıralama algoritmasındaki dizideki değeri küçük olan elemanların dizinin başında kümelenmesi yöntemine benzer şekilde gerçekleşir.
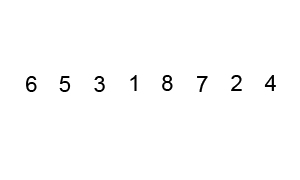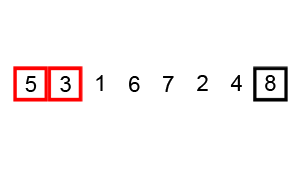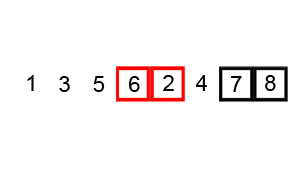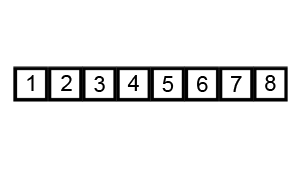
public void BubbleSort(int[] array)
{
int n = array.Length;
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n - i - 1; j++)
{
if (array[j] > array[j + 1])
{
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
}
}
– Eklemeli Sıralama (Insertion sort)
Eklemeli sıralama, elinizdeki oyun kartlarını sıralama şeklinize benzer şekilde çalışan basit bir sıralama algoritmasıdır. Dizi sanal olarak sıralanmış ve sıralanmamış bir parçaya bölünmüştür. Sıralanmamış kısımdaki değerler alınır ve sıralanan kısımdaki doğru konuma yerleştirilir.

public void InsertionSort(int[] array)
{
int n = array.Length;
for (int i = 1; i < n; i++)
{
int key = array[i];
int j = i - 1;
while (j >= 0 && array[j] > key)
{
array[j + 1] = array[j];
j = j - 1;
}
array[j + 1] = key;
}
}
– Birleştirmeli Sıralama (Merge Sort)
Girdi olarak aldığı diziyi en küçük hale gelene kadar ikili gruplara böler ve karşılaştırma yöntemi kullanarak diziyi sıralar.

using System;
class SortingAlgorithms {
void merge(int[] arr, int l, int m, int r)
{
int n1 = m - l + 1;
int n2 = r - m;
int[] L = new int[n1];
int[] R = new int[n2];
int i, j;
for (i = 0; i < n1; ++i)
L[i] = arr[l + i];
for (j = 0; j < n2; ++j)
R[j] = arr[m + 1 + j];
i = 0;
j = 0;
int k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
}
else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
void sort(int[] arr, int l, int r)
{
if (l < r) {
int m = l + (r - l) / 2;
sort(arr, l, m);
sort(arr, m + 1, r);
merge(arr, l, m, r);
}
}
static void printArray(int[] arr)
{
int n = arr.Length;
for (int i = 0; i < n; ++i)
Console.Write(arr[i] + " ");
Console.WriteLine();
}
public static void Main(String[] args)
{
int[] arr = { 12, 11, 13, 5, 6, 7 };
Console.WriteLine("Given Array");
printArray(arr);
MergeSort ob = new MergeSort();
ob.sort(arr, 0, arr.Length - 1);
Console.WriteLine("\nSorted array");
printArray(arr);
}
}
– Hızlı Sıralama (Quick Sort)
Hızlı sıralama, bir pivot elemanını seçerek listeyi pivot elemanından küçük ve büyük olmak üzere ikiye böler. Her ikiye bölünmüş alt liste için aynı işlemi tekrar ederek sıralama işlemi gerçekleştirilir.
public void QuickSort(int[] array, int low, int high)
{
if (low < high)
{
int pi = Partition(array, low, high);
QuickSort(array, low, pi - 1);
QuickSort(array, pi + 1, high);
}
}
private int Partition(int[] array, int low, int high)
{
int pivot = array[high];
int i = low - 1;
for (int j = low; j < high; j++)
{
if (array[j] < pivot)
{
i++;
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
int temp2 = array[i + 1];
array[i + 1] = array[high];
array[high] = temp2;
return i + 1;
}
Her bir algoritma, farklı zaman ve hafıza karmaşıklıklarına sahip olabilir, bu yüzden kullanım senaryonuza ve ihtiyaçlarınıza bağlı olarak en uygun olanı seçebilirsiniz.